6.3. Logaritmisku vienādojumu atrisināšana, logaritmējot vienādojuma abas puses
Ja logaritmiskā vienādojumā nezināmais atrodas gan
pakāpes bāzē, gan kāpinātājā, šādus vienādojumus risina, abas puses logaritmējot.
Logaritmēt nozīmē – aprēķināt logaritmus pie vienas un tās pašas bāzes abām vienādojuma pusēm.
Piemērs
Atrisināt vienādojumu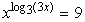 
.
|
Soļi
|
Risinājums
|
| Lai atbrīvotos no logaritma kāpinātājā, abas vienādojuma puses logaritmē pie bāzes 3, jo šādas bāzes logaritms jau ir vienādojumā
|
|
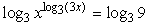
| Izmanto logaritmu īpašības
|
log3 (3x) · log3 x = 2
(log3 3 + log3 x) · log3
x= 2
(1 + log3 x)
· log3 x = 2 |
| Izmanto substitūcijas metodi. Apzīmē log3
x = t
|
(1 + t) · t = 2
|
| Atrisina algebrisko vienādojumu
|
t2 + t
– 2 = 0
t1 = - 2 un t2 = 1
|
| Atgriežas pie apzīmētās izteiksmes
|
log3 x = - 2 vai
log3 x = 1
|
| Atrisina logaritmiskos vienādojumus
|
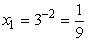 vai x2 = 31 = 3, abas saknes ietilpst vienādojuma definīcijas apgabalā x > 0
|