2. uzdevums

Vienādsānu trijstūra pamata garums ir 12 cm, bet augstums pret pamatu ir 8 cm. Trijstūrī ievilkta riņķa līnija un tai novilkta pieskare paralēli trijstūra pamatam. Nosaki pieskares nogriežņa garumu, kas atrodas starp trijstūra sānu malām!

Atrisinājums

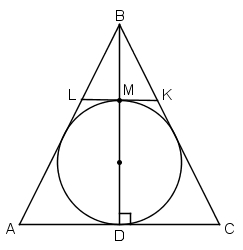
Dots: trijstūris ABC, kur AB=BC un AC=12 cm. BD=8 cm, kur BD augstums. KL – trijstūrī ievilktas riņķa līnijas pieskare un KL||AC. Jāaprēķina: KL
Tālāk

Viens no iespējamiem risinājumiem balstās uz trijstūru ABC un LBK līdzību (tas ir jāpamato). Lai to izmantotu, jānosaka BM garums.
Ieteicams sastādīt risinājuma plānu

1. Aprēķina trijstūra sānu malas garumu, izmantojot Pitagora teorēmu.
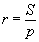
2. Aprēķina riņķa līnija rādiusu, izmantojot formulu, kur S-trijstūra laukums un p - trijstūra pusperimetrs .
3. Aprēķina BM garumu kā BD un MD garumu starpību.
4. Pamato, ka trijstūri ABC un LBK ir līdzīgi.
5. Aprēķina KL, izmantojot trijstūru ABC un LBK ir līdzību.

Tālāk
Tā kā trijstūris ABC ir vienādsānu, BD ir arī mediāna un AD = 6 cm. Pēc Pitagora teorēmas trijstūrī ABD

AB2= 82+ 62= 64 + 36 = 100
AB = 10 cm
 
Tālāk

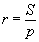
Lai izmantotu formulu , jānosaka trijst;ura ABC pusperimetrs un laukums


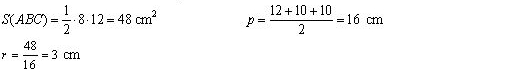Tālāk
BM= BD – DM = 8 – 6 = 2 cm
Tālāk
ABC ~ LBK pēc pazīmes (ll), jo:
• leņķis B ir kopīgs ;
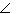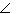• BAC=BLK kā kāpšļu leņķi pie paralēlām taisnēm .
Tālāk


Līdzīgu trijstūru ABC un LBK atbilstošie nogriežņi ir proporcionāli.
Proporcijā ievietojot skaitļus, iegūst skaitlisku proporciju.
Izsaka  LK;   


Tālāk
Atbilde: KL = 3 cm